Hi all: Homework 5 has been posted on the webpage. It’s based on Chernoff bounds, some streaming, and a proof of a matrix Chernoff bound, and is due on March 20th. (In 2 weeks or so.)
Questions and comments below!
P.S. If you haven’t see the Lowner ordering before, solve exercise 4 before you start on problem 5.
15-850: CMU Advanced Algorithms 
Is there a reason problem 5 is in parentheses?
LikeLike
No reason, just a slip in typesetting….
LikeLike
Okay thanks! I also was wondering: in problem 4.b., we define S_n as sum(X1, X2, …, Xn). Is the same definition used on the left and right side of the equation? Or is S_n redefined as sum(X1, X2, …, X_(n-1)) on the right?
If both sides use the same definition, it seems like weird things happen…the left side side is not a function of X_n because the Expected Value “integrates away” the X_n term, but that doesn’t happen on the right side. So the right side would still be a function of X_n.
LikeLike
Sorry, it’s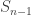
on the right. Fixing it right now.
LikeLike
On the same problem, should there also be a t in the exponents in the first two expectations? Or does that turn out to not matter?
LikeLike
There should indeed be a
in those. Will fix, thanks David!
LikeLike
Also I’m a little confused on 5.(a).I feel like I’ve found a contradiction which usually means I misunderstood something
Suppose R=1/4. Suppose the matrices are 1×1.
Suppose Y_i= {R} = {1/4}
Suppose E[Y_i] = U_i = {1}
X_i = {1/4-1} = {(1/4-1)/(1/4)} = {3}
X_i * X_i = {9}
The biggest eigenvalue of X_i*X_i is 9, so the 2-norm of X_i is 3, which is more than 1.
Did I do something wrong here? Is there some way to ensure R>1/2?
LikeLike
I see the confusion: when we say
we mean all outcomes of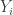 
have spectral value at most 
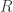. Much like saying ![Y_i \in [0,1]](https://s0.wp.com/latex.php?latex=Y_i+%5Cin+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002)
. In your example where ![E[Y_i] = 1](https://s0.wp.com/latex.php?latex=E%5BY_i%5D+%3D+1&bg=ffffff&fg=333333&s=0&c=20201002)
, then there must be some other outcomes where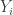 
is large.
LikeLike
Thanks! Hopefully my last question for a while:
In part 1.b., I have a solution that works for N = 1/1000000 \epsilon^2 d but does not work for N=99999 \epsilon^2 d. Is that acceptable?
I think that is a correct interpretation of the Omega notation but wanted to double check before writing the whole thing out.
LikeLike
That is indeed acceptable!
LikeLike
What is the definition of 2-universal hash family in problem 2? From what I look up, it satisfies Pr(h(x) != h(y)) <= 1/N for all x != y. But that isn't sufficient, because h(0) could always be 0, and the tester would always return High. Should we assume that Pr(h(x) = y) = 1/N for all y?
LikeLike
sorry, for the last sentence, I meant:
But that isn’t sufficient, because h(0) could always be 0, and the tester would always return High if 0 is in the stream. Should we assume in addition that Pr(h(x) = y) = 1/N for all y?
LikeLike
oops, sorry, I realized that it’s also defined in the lecture notes, and that we can indeed assume that.
LikeLike
Love these comments that answer themselves! 🙂 Indeed, the definition is in Lecture 20 (section 2.1.1) and folds in the idea of being uniform on single elements, and being pairwise independent.
LikeLike
Just a note to others, when doing Exercise 4 on this homework, be sure to apply functions as defined here: http://www.cs.cmu.edu/~anupamg/advanced/lectures/lecture21.pdf#page=7
f(A) does not denote, for instance, entrywise application.
LikeLike
For problem 4c, it looks if you directly use 4(a) and 4(b) you don’t get a factor of d anywhere….
LikeLike
Ignore my last comment, I messed up my calculations
LikeLike
Is there an analog of 4.c. for expectation?
Something like:
Let x be a real number given from some probability distribution such that x is always in the range [a,b], and E[f(x)]<= g(x)
Similarly let A be given by some probability distribution such that its eigenvalues are always in the range [a,b].
From this we conclude E[f(A)]<= g(A)
I don't recall seeing this theorem anywhere yet but it feels very natural. The problem is that E[f(A)] isn't actually a function of A, which makes weird things happen.
LikeLike